目錄
博客: | |
權重初始化最佳實踐
書接上回,全0、常數、過大、過小的權重初始化都是不好的,那我們需要什麼樣的初始化?
- 因為對權重\(w\)的大小和正負缺乏先驗,所以應初始化在0附近,但不能為全0或常數,所以要有一定的隨機性,即數學期望\(E(w)=0\);
-
因為梯度消失和梯度爆炸,權重不易過大或過小,所以要對權重的方差\(Var(w)\)有所控制;
- 深度神經網絡的多層結構中,每個激活層的輸出對後面的層而言都是輸入,所以我們希望不同激活層輸出的方差相同,即\(Var(a^{[l]})=Var(a^{[l-1]})\),這也就意味不同激活層輸入的方差相同,即\(Var(z^{[l]})=Var(z^{[l-1]})\);
-
如果忽略激活函數,前向傳播和反向傳播可以看成是權重矩陣(轉置)的連續相乘。數值太大,前向時可能陷入飽和區,反向時可能梯度爆炸,數值太小,反向時可能梯度消失。所以初始化時,權重的數值範圍(方差)應考慮到前向和後向兩個過程;
權重的隨機初始化過程可以看成是從某個概率分佈隨機採樣的過程,常用的分佈有高斯分佈、均勻分佈等,對權重期望和方差的控制可轉化為概率分佈的參數控制,權重初始化問題也就變成了概率分佈的參數設置問題。
在上回中,我們知道反向傳播過程同時受到權重矩陣和激活函數的影響,那麼,在激活函數不同以及每層超參數配置不同(輸入輸出數量)的情況下,權重初始化該做怎樣的適配?這裏,將各家的研究成果匯總如下,
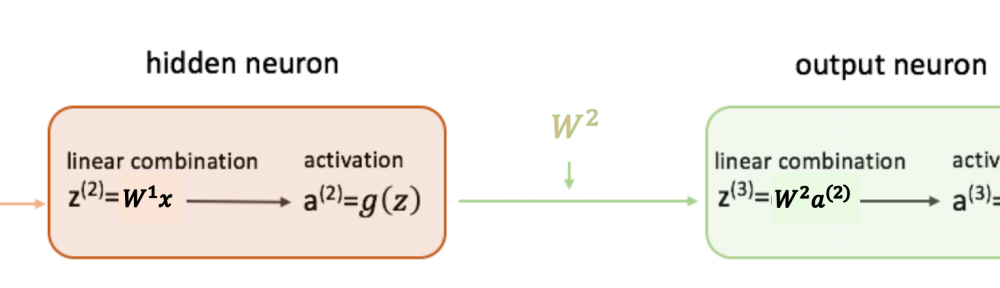
其中,扇入\(fan\_in\)和扇出\(fan\_out\)分別為當前全連接層的輸入和輸出數量,更準確地說,1個輸出神經元與\(fan\_in\)個輸入神經元有連接(the number of connections feeding into the node),1個輸入神經元與\(fan\_out\)個輸出神經元有連接(the number of connections flowing out of the node),如下圖所示(來自),
對於卷積層而言,其權重為\(n\)個\(c\times h \times w\)大小的卷積核,則一個輸出神經元與\(c\times h \times w\)個輸入神經元有連接,即\(fan\_in = c\times h \times w\),一個輸入神經元與\(n\times h \times w\)個輸出神經元有連接,即\(fan\_out=n\times h \times w\)。
期望與方差的相關性質
接下來,首先回顧一下期望與方差計算的相關性質。
對於隨機變量\(X\),其方差可通過下式計算,
\[ Var(X) = E(X^2) – (E(X))^2 \]
若兩個隨機變量\(X\)和\(Y\),它們相互獨立,則其協方差為0,
\[ Cov(X, Y) = 0 \]
進一步可得\(E(XY)=E(X)E(Y)\),推導如下,
\[ \begin{align} Cov(X, Y) &= E((X-E(X))(Y-E(Y))) \\ &= E(XY)-E(X)E(Y) =0 \end{align} \]
兩個獨立隨機變量和的方差,
\[ \begin{aligned} \operatorname{Var}(X+Y) &=E\left((X+Y)^{2}\right)-(E(X+Y))^{2} \\ &=E\left(X^{2}+Y^{2}+2 X Y\right)-(E(X)+E(Y))^{2} \\ &=\left(E\left(X^{2}\right)+E\left(Y^{2}\right)+2 E(X Y)\right)-\left((E(X))^{2}+(E(Y))^{2}+2 E(X) E(Y)\right) \\ &=\left(E\left(X^{2}\right)+E\left(Y^{2}\right)+2 E(X) E(Y)\right)-\left((E(X))^{2}+(E(Y))^{2}+2 E(X) E(Y)\right) \\ &=E\left(X^{2}\right)-(E(X))^{2}+E\left(Y^{2}\right)-(E(Y))^{2} \\ &=\operatorname{Var}(X)+\operatorname{Var}(Y) \end{aligned} \]
兩個獨立隨機變量積的方差,
\[ \begin{aligned} \operatorname{Var}(X Y) &=E\left((X Y)^{2}\right)-(E(X Y))^{2} \\ &=E\left(X^{2}\right) E\left(Y^{2}\right)-(E(X) E(Y))^{2} \\ &=\left(\operatorname{Var}(X)+(E(X))^{2}\right)\left(\operatorname{Var}(Y)+(E(Y))^{2}\right)-(E(X))^{2}(E(Y))^{2} \\ &=\operatorname{Var}(X) \operatorname{Var}(Y)+(E(X))^{2} \operatorname{Var}(Y)+\operatorname{Var}(X)(E(Y))^{2} \end{aligned} \]
全連接層方差分析
對線性組合層+非線性激活層,計算如下所示,其中\(z_i^{[l-1]}\)為\(l-1\)層第\(i\)個激活函數的輸入,\(a_i^{[l-1]}\)為其輸出,\(w_{ij}^{[l]}\)為第\(l\)層第\(i\)個輸出神經元與第\(j\)個輸入神經元連接的權重,\(b^{[l]}\)為偏置,計算方式如下
\[ \begin{align}a_i^{[l-1]} &= f(z_i^{[l-1]}) \\z_i^{[l]} &= \sum_{j=1}^{fan\_in} w_{ij}^{[l]} \ a_j^{[l-1]}+b^{[l]} \\a_i^{[l]} &= f(z_i^{[l]})\end{align} \]
在初始化階段,將每個權重以及每個輸入視為隨機變量,可做如下假設和推斷,
- 網絡輸入的每個元素\(x_1,x_2,\dots\)為獨立同分佈;
- 每層的權重隨機初始化,同層的權重\(w_{i1}, w_{i2}, \dots\)獨立同分佈,且期望\(E(w)=0\);
- 每層的權重\(w\)和輸入\(a\)隨機初始化且相互獨立,所以兩者之積構成的隨機變量\(w_{i1}a_1, w_{i2}a_2, \dots\)亦相互獨立,且同分佈;
- 根據上面的計算公式,同層的\(z_1, z_2, \dots\)為獨立同分佈,同層的\(a_1, a_2, \dots\)也為獨立同分佈;
需要注意的是,上面獨立同分佈的假設僅在初始化階段成立,當網絡開始訓練,根據反向傳播公式,權重更新后不再相互獨立。
在初始化階段,輸入\(a\)與輸出\(z\)方差間的關係如下,令\(b=0\),
\[ \begin{align} Var(z) &=Var(\sum_{j=1}^{fan\_in} w_{ij} \ a_j) \\ &= fan\_in \times (Var(wa)) \\ &= fan\_in \times (Var(w) \ Var(a) + E(w)^2 Var(a) + Var(w) E(a)^2) \\ &= fan\_in \times (Var(w) \ Var(a) + Var(w) E(a)^2) \end{align} \]
tanh下的初始化方法
若激活函數為線性恆等映射,即\(f(x)=x\),則\(a = z\),自然\(E(a)=E(z)\),\(Var(a) = Var(z)\)。
因為網絡輸入的期望\(E(x)=0\),每層權重的期望\(E(w) = 0\),在前面相互獨立的假設下,根據公式\(E(XY)=E(X)E(Y)\),可知\(E(a)=E(z)=\sum E(wa)=\sum E(w)E(a)=0\)。由此可得,
\[ Var(a^{[l]}) = Var(z^{[l]}) = fan\_in \times Var(w) \times Var(a^{[l-1]}) \]
更進一步地,令\(n^{[l]}\)為第\(l\)層的輸出數量(\(fan\_out\)),則第\(l\)層的輸入數量($fan_in \()即前一層的輸出數量為\)n^{[l-1]}\(。第\)L$層輸出的方差為
\[ \begin{align} Var(a^{L}) = Var(z^{[L]}) &= n^{[L-1]} Var(w^{[L]}) Var(a^{[L-1]}) \\ &=\left[\prod_{l=1}^{L} n^{[l-1]} Var(w^{[l]})\right] {Var}(x) \end{align} \]
反向傳播時,需要將上式中的\(n^{[l-1]}\)替換為\(n^{[l]}\)(即\(fan\_in\)替換為\(fan\_out\)),同時將\(x\)替換為損失函數對網絡輸出的偏導。
所以,經過\(t\)層,前向傳播和反向傳播的方差,將分別放大或縮小
\[ \prod^{t} n^{[l-1]} Var(w^{[l]}) \\ \prod^{t} n^{[l]} Var(w^{[l]}) \]
為了避免梯度消失和梯度爆炸,最好保持這個係數為1。
需要注意的是,上面的結論是在激活函數為恆等映射的條件下得出的,而tanh激活函數在0附近可近似為恆等映射,即$tanh(x) \approx x $。
Lecun 1998
Lecun 1998年的paper ,在輸入Standardization以及採用tanh激活函數的情況下,令\(n^{[l-1]}Var(w^{[l]})=1\),即在初始化階段讓前向傳播過程每層方差保持不變,權重從如下高斯分佈採樣,其中第\(l\)層的\(fan\_in = n^{[l-1]}\),
\[ W \sim N(0, \frac{1}{fan\_in}) \]
Xavier 2010
在paper 中,Xavier和Bengio同時考慮了前向過程和反向過程,使用\(fan\_in\)和\(fan\_out\)的平均數對方差進行歸一化,權重從如下高斯分佈中採樣,
\[ W \sim N(0, \frac{2}{fan\_in + fan\_out}) \]
同時文章中還提及了從均勻分佈中初始化的方法,因為均勻分佈的方差與分佈範圍的關係為
\[ Var(U(-n, n)) = \frac{n^2}{3} \]
若令\(Var(U(-n, n)) = \frac{2}{fan\_in + fan\_out}\),則有
\[ n = \frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}} \]
即權重也可從如下均勻分佈中採樣,
\[ W \sim U(-\frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}}, \frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}}) \]
在使用不同激活函數的情況下,是否使用Xavier初始化方法對test error的影響如下所示,圖例中帶\(N\)的表示使用Xavier初始化方法,Softsign一種為類tanh但是改善了飽和區的激活函數,圖中可以明顯看到tanh 和tanh N在test error上的差異。
論文還有更多訓練過程中的權重和梯度對比圖示,這裏不再貼出,具體可以參見論文。
ReLU/PReLU下的初始化方法
搬運一下上面的公式,
\[ Var(z)= fan\_in \times (Var(w) \ Var(a) + Var(w) E(a)^2) \]
因為激活函數tanh在0附近可近似為恆等映射,所以在初始化階段可以認為\(E(a) = 0\),但是對於ReLU激活函數,其輸出均大於等於0,不存在負數,所以\(E(a) = 0\)的假設不再成立。
但是,我們可以進一步推導得到,
\[ \begin{align} Var(z) &= fan\_in \times (Var(w) \ Var(a) + Var(w) E(a)^2) \\ &= fan\_in \times (Var(w) (E(a^2) – E(a)^2)+Var(w)E(a)^2) \\ &= fan\_in \times Var(w) \times E(a^2) \end{align} \]
He 2015 for ReLU
對於某個具體的層\(l\)則有,
\[ Var(z^{[l]}) = fan\_in \times Var(w^{[l]}) \times E((a^{[l-1]})^2) \]
如果假定\(w{[l-1]}\)來自某個關於原點對稱的分佈,因為\(E(w^{[l-1]}) = 0\),且\(b^{[l-1]} = 0\),則可以認為\(z^{[l-1]}\)分佈的期望為0,且關於原點0對稱。
對於一個關於原點0對稱的分佈,經過ReLU后,僅保留大於0的部分,則有
\[ \begin{align}Var(x) &= \int_{-\infty}^{+\infty}(x-0)^2 p(x) dx \\&= 2 \int_{0}^{+\infty}x^2 p(x) dx \\&= 2 E(\max(0, x)^2)\end{align} \]
所以,上式可進一步得出,
\[ \begin {align}Var(z^{[l]}) &= fan\_in \times Var(w^{[l]}) \times E((a^{[l-1]})^2) \\&= \frac{1}{2} \times fan\_in \times Var(w^{[l]}) \times Var(z^{[l-1]}) \end{align} \]
類似地,需要放縮係數為1,即
\[ \frac{1}{2} \times fan\_in \times Var(w^{[l]}) = 1 \\ Var(w) = \frac{2}{fan\_in} \]
即從前向傳播考慮,每層的權重初始化為
\[ W \sim N(0, \frac{2}{fan\_in}) \]
同理,從後向傳播考慮,每層的權重初始化為
\[ W \sim N(0, \frac{2}{fan\_out}) \]
文中提到,單獨使用上面兩个中的哪一個都可以,因為當網絡結構確定之後,兩者對方差的放縮係數之比為常數,即每層扇入扇出之比的連乘,解釋如下,
使用Xavier和He初始化,在激活函數為ReLU的情況下,test error下降對比如下,22層的網絡,He的初始化下降更快,30層的網絡,Xavier不下降,但是He正常下降。
He 2015 for PReLU
對於PReLU激活函數,負向部分為\(f(x) = ax\),如下右所示,
對於PReLU,求取\(E((a^{[l-1]})^2)\)可對正向和負向部分分別積分,不難得出,
\[ \frac{1}{2} (1 + a^2) \times fan\_in \times Var(w^{[l]}) = 1 \\Var(w) = \frac{2}{(1 + a^2) fan\_in} \\W \sim N(0, \frac{2}{(1 + a^2) fan\_in}) \\W \sim N(0, \frac{2}{(1 + a^2) fan\_out}) \]
caffe中的實現
儘管He在paper中說單獨使用\(fan\_in\)或\(fan\_out\)哪個都可以,但是,在Caffe的實現中,還是提供了兩者平均值的方式,如下所示,當然默認是使用\(fan\_in\)。
小結
至此,對深度神經網絡權重初始化方法的介紹已告一段落。雖然因為BN層的提出,權重初始化可能已不再那麼緊要。但是,對經典權重初始化方法經過一番剖析后,相信對神經網絡運行機制的理解也會更加深刻。
以上。
參考
本站聲明:網站內容來源於博客園,如有侵權,請聯繫我們,我們將及時處理
【其他文章推薦】
※台北網頁設計公司這麼多,該如何挑選?? 網頁設計報價省錢懶人包”嚨底家”
※網頁設計公司推薦更多不同的設計風格,搶佔消費者視覺第一線
※想知道購買電動車哪裡補助最多?台中電動車補助資訊懶人包彙整